It is frequent to see the following three terms in machine learning: normalization, standardization and regularization. Here comes a short introduction to help to distinguish them.

Normalization

Normalization usually rescales features to \([0, 1]\).1 That is,

\[x' = \dfrac{x - min(x)}{max(x) - min(x)}\]

It will be useful when we are sure enough that there are no anomalies (i.e. outliers) with extremely large or small values. For example, in a recommender system, the ratings made by users are limited to a small finite set like \(\{1, 2, 3, 4, 5\}\).

In some situations, we may prefer to map data to a range like \([-1, 1]\) with zero-mean.2 Then we should choose mean normalization.3

\[x' = \dfrac{x - mean(x)}{max(x) - min(x)}\]

In this way, it will be more convenient for us to use other techniques like matrix factorization.

Standardization

Standardization is widely used as a preprocessing step in many learning algorithms to rescale the features to zero-mean and unit-variance.3

\[x' = \dfrac{x - \mu}{\sigma}\]

Regularization

Different from the feature scaling techniques mentioned above, regularization is intended to solve the overfitting problem. By adding an extra part to the loss function, the parameters in learning algorithms are more likely to converge to smaller values, which can significantly reduce overfitting.

There are mainly two basic types of regularization: L1-norm (lasso) and L2-norm (ridge regression).4

L1-norm

The original loss function is denoted by \(f(x)\), and the new one is \(F(x)\).

\[F(x) = f(x) + \lambda {\lVert x \rVert}_1\]

where

\[{\lVert x \rVert}_p = \sqrt[p]{\sum_{i = 1}^{n} {\lvert x_i \rvert}^p}\]

L1 regularization is better when we want to train a sparse model, since the absolute value function is not differentiable at 0.5

L2-norm

\[F(x) = f(x) + \lambda {\lVert x \rVert}_2^2\]

L2 regularization is preferred in ill-posed problems for smoothing.5

Here is a comparison between L1 and L2 regularizations.

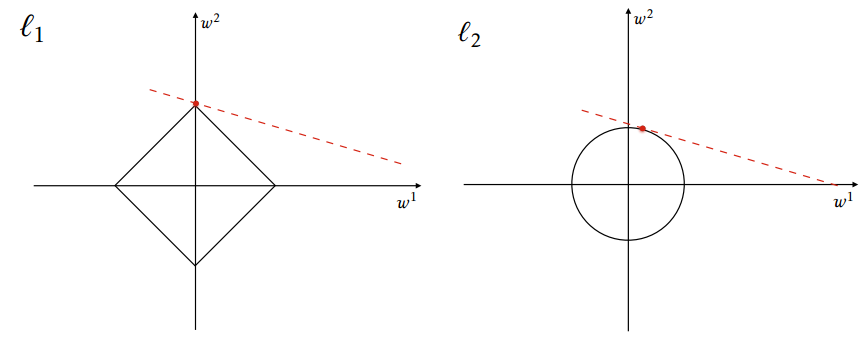comparison between L1 and L2 From https://en.wikipedia.org/wiki/Regularization_(mathematics)

References

  1. https://stats.stackexchange.com/a/10298 ↩

  2. https://www.quora.com/What-is-the-difference-between-normalization-standardization-and-regularization-for-data/answer/Enzo-Tagliazucchi ↩

  3. https://en.wikipedia.org/wiki/Feature_scaling ↩ ↩2

  4. https://en.wikipedia.org/wiki/Regularization_%28mathematics%29 ↩

  5. https://www.quora.com/What-is-the-difference-between-L1-and-L2-regularization-How-does-it-solve-the-problem-of-overfitting-Which-regularizer-to-use-and-when/answer/Kenneth-Tran ↩ ↩2